一 系统端口分析简介

1 输入阻抗和输出阻抗

　　对于如下所示的二端口网络，输入阻抗由欧姆定律定义如下：

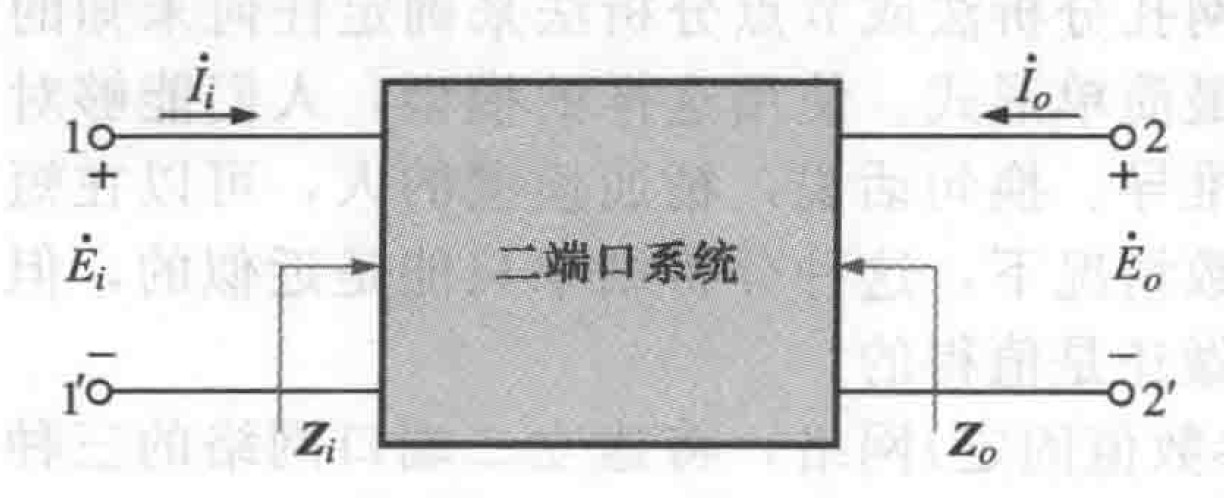图1 输入阻抗和输出阻抗的定义
$$ Z_i=\frac{\dot{E_i}}{\dot{I_i}} \tag{1} $$

　　输出阻抗定义为将输入电压置零时：

$$ Z_o=\frac{\dot{E_o}}{\dot{I_o}} \tag{2} $$

　　需要注意，$\dot{I_i}$和$\dot{I_o}$定义为流入二端口网络的电流，为了避免对电流实际方向的关注，在系统的端口分析方法中总是做这样的规定。

2 空载与有载电压增益

　　本章研究的是交流系统，因此电压电流等符号上面都应该加一个点，但是在写latex公式时如果对每个符号都这样做实在太麻烦，因此约定后面的符号都不加点，但请注意他们是复数，不是相量。

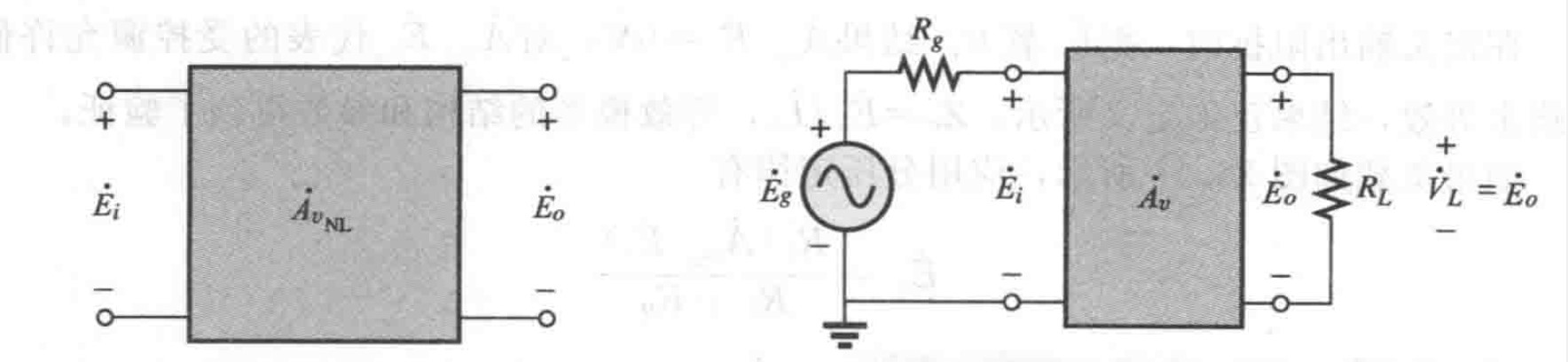图2 空载和有载电压增益的定义

　　二端口网络的电压增益定义为：

$$ A_{v_{NL}}=\frac{E_o}{E_i} \tag{3} $$

　　式中下标V表示电压，下标NL表示无负载即空载情况，空载电压增益是二端口网络提供的增益。
　　若在二端口网络接入一个负载，得到带负载的增益，简单表示为$A_V$，定义为：

$$ A_v=\frac{E_o}{E_i}|_{含R_L} \tag{4} $$

　　对于所有的二端口网络，有载增益A_V总是小于空载增益，换句话说，负载总会使增益减小，小于空载增益。
　　如果考虑电压源中的内阻，则二端口网络等效为图2中所示，当考虑这个电阻之后，总的电压增益定义为：

$$ A_{v_T}=\frac{E_o}{E_g}\tag{5} $$

　　电压增益$A_{V_T}$总是小于有载电压增益$A_V$或空载电压增益$A_{V_{NL}}$

3 电流增益及功率增益

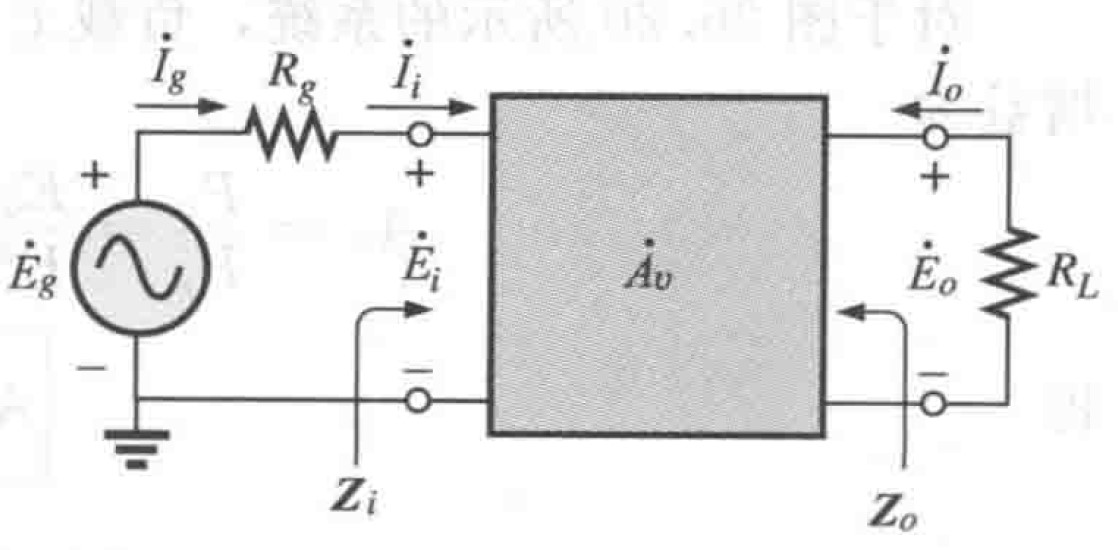图3 电流增益

　　二端口网络的电流增益通常是用电压来计算的。

$$ A_i=\frac{I_o}{I_i}=\frac{E_o/R_L}{E_i/Z_L}=-A_v\frac{Z_i}{R_L}\tag{6} $$

　　功率增益为：

$$ A_G=\frac{P_o}{P_i}=|A_v||A_i|\tag{7} $$

4 二端口网络的级联

　　对于二端口网络的级联，应该记住，级联网络的公式要使用每一级的有载电压增益和电流增益，而不是铭牌上的空载增益。

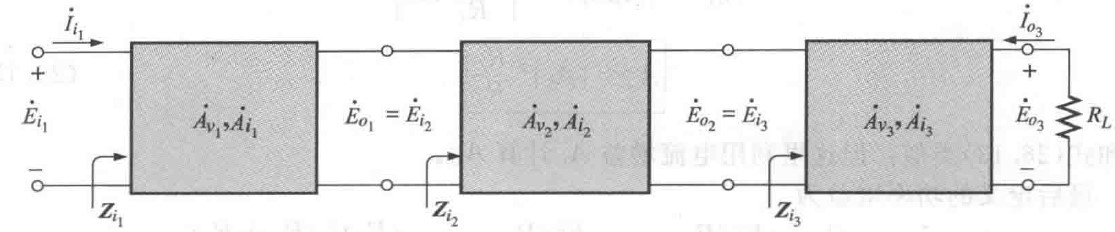图4 二端口网络的级联

　　上图所示的级联网络的总电压增益为：

$$ A_{v_T}=A_{v_1}A_{v_2}A_{v_3}\tag{8} $$

　　级联网络的总电流增益是：

$$ A_{i_T}=A_{i_1}A_{i_2}A_{i_3}\tag{9} $$

5 阻抗参数、导纳参数、混合参数

　　对于如下所示的二端口网络，给出了四个端口变量，这四个变量的关系可以用下面的公式来表示：

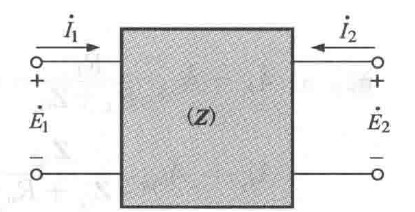图5 二端口阻抗的网络参数
$$ E_1=Z_{11}I_1+Z_{12}I_2\tag{10} $$
$$ E_2=Z_{21}I_1+Z_{22}I_2\tag{11} $$

$Z_{11}$称为开路输入阻抗，$Z_{12}$为开路反向转移阻抗，$Z_{21}$为开路前向转移阻抗，$Z_{22}$为开路输出阻抗。

$$ I_1=y_{11}E_1+y_{12}E_2\tag{12} $$
$$ I_2=y_{21}E_1+y_{22}E_2\tag{13} $$

　　$y_{11}$为短路输入导纳，$y_{12}$为短路反向转移导纳，$y_{21}$为短路前向转移导纳，$y_{22}$为短路输出导纳。
　　混合参数被广泛用于晶体管电路的分析。“混合”主要是因为这种参数的单位是混合的，不像阻抗参数单位都是欧姆，也不像导纳参数，单位都是西门子。

$$ E_1=h_{11}I_1+h_{12}E_2\tag{14} $$
$$ I_2=h_{21}I_1+h_{22}E_2\tag{15} $$

　　$h_{11}$为短路输入阻抗，$h_{12}$为开路反向转移电压比，$h_{21}$为短路前向转移电流比，$h_{22}$为开路输出导纳。在很多应用场合，混合参数的下标可以做如下简化：$h_{11}=h_i$，$h_{12}=h_r$，$h_{21}=h_f$，$h_{22}=h_o$

6 z、y、h参数之间的相互转化

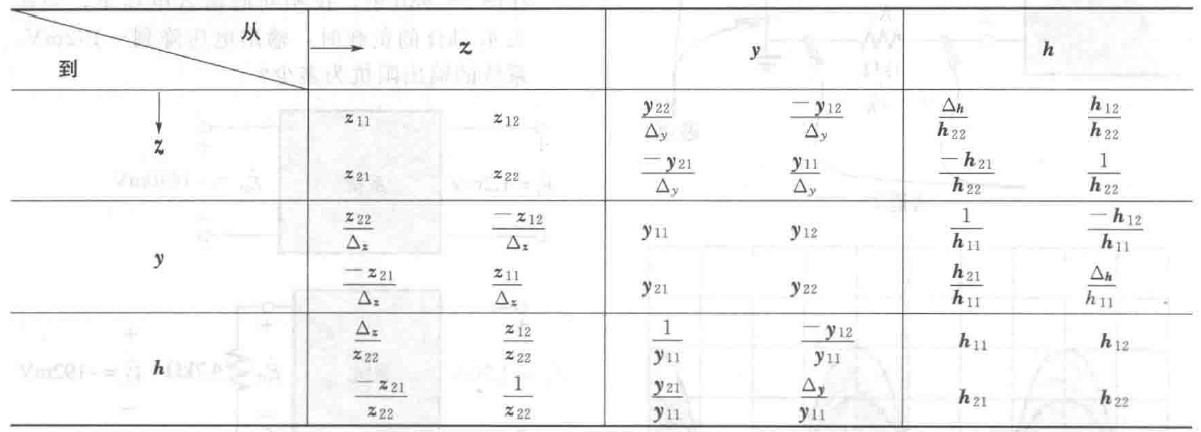图6 zyh参数之间的相互转化