一 谐振电路

1 谐振电路简介

　　谐振电路（又称调谐电路），谐振电路是由RLC元件构成的具有类似下图所示的频率特性的电路，频率在$f_r$处电压或电流的相应最大，而在此频率左右两侧电压或电流是衰减的，换句话说，在特定频率范围内，响应接近或等于此最大值，在该频率的左右两侧较远处，电压或电流非常小（实际应用中，这种微弱的响应对系统几乎不产生影响），这个原理广泛应用于收音机、广播电台，这也是把谐振电路称为调谐电路的原因，当响应处于或接近于最大值时，称电路处于谐振状态，此时电路端口的电压U和电流I出现同相位，电路呈电阻性。

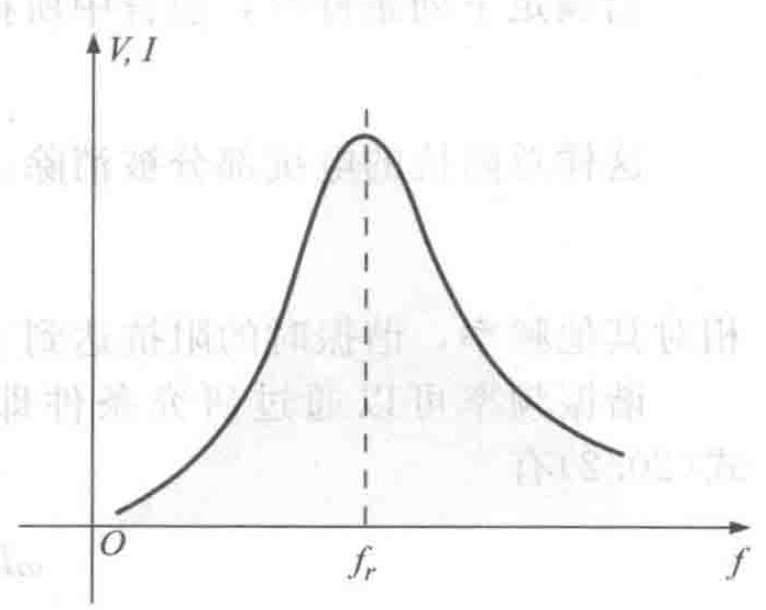图1 谐振曲线

　　谐振的实质是电容中的电场能与电感中的磁场能相互转换，此增彼减，完全补偿，电场能和磁场能的总和时刻保持不变，电源不必与电容或电感往返转换能量，只需供给电路中电阻所消耗的能量。

2 串联谐振电路

　　一个谐振电路（不管串联或并联）必须含有电感和电容元件，对于串联谐振电路，还包括电源内阻$R_s$、电感的固有电阻$R_L$，以及专门用来控制谐振曲线而接入的电阻$R_d$，将这三种电阻合并为：

$$ R=R_s+R_L+R_d \tag{1} $$
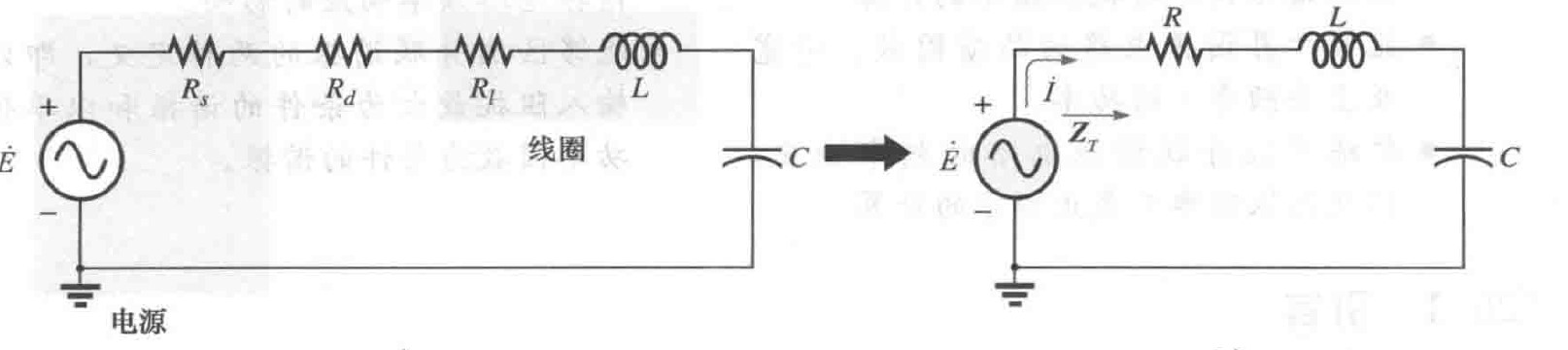图2 串联谐振电路

　　在任意频率下，总阻抗$Z_T=R+j(X_C-X_L)$满足下式，就会发生谐振：

$$ X_L=X_C \tag{2} $$

　　这时总阻抗的电抗部分被消除，此时谐振总阻抗为$Z_T=R$，好像电路中只有一个电阻一样，解公式（2）得到谐振角频率

$$ \omega _s= \frac{1}{\sqrt {LC}} \tag{3} $$

　　谐振频率为：

$$ f_s= \frac{1}{2\pi \sqrt {LC}} \tag{4} $$

　　此时电阻上的电压就是输入电压，总视在功率等于电阻上的有功功率，功率三角形中电感和电容上的无功功率分别是$I^{2}X_L$、$I^{2}X_C$,电路总的无功功率为零，电路的功率因素为1。

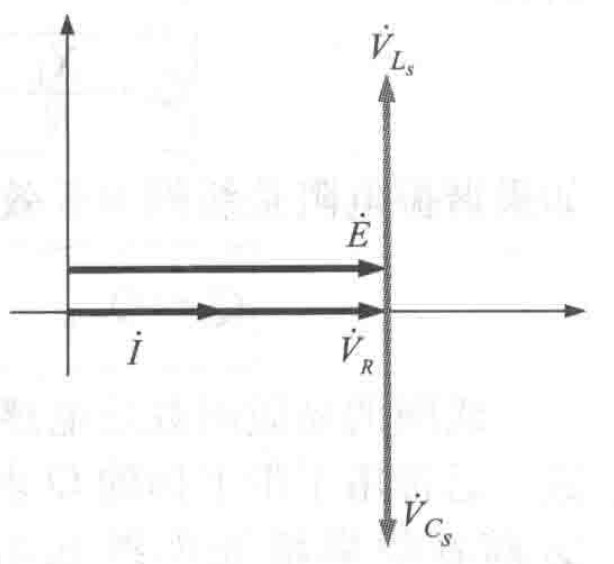图3 串联谐振电路谐振时的相量图

　　从串联谐振电路谐振时的功率曲线图可以看出，电感和电容的能量相互吸收和释放，一部分能量反复在电感和电容之间转移，在电源的角度看，无功功率为零。

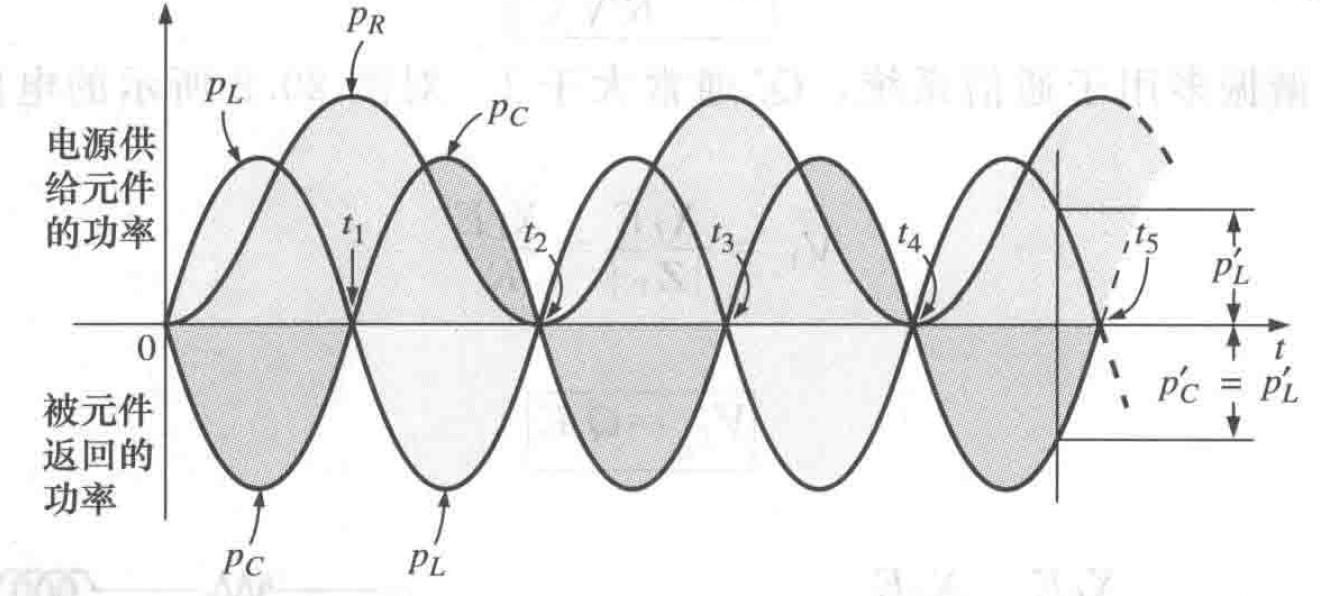图4 串联谐振电路谐振时的功率曲线

3 品质因数

　　串联谐振电路的品质因素定义为谐振时电感或电容上的无功功率与电阻上的有功功率之比，即

$$ Q_S=\frac{无功功率}{有功功率}=\frac{I^2X_L}{I^2R} =\frac{X_L}{R} = \frac{L}{R\sqrt{LC}} \tag{5} $$

　　串联谐振多用于通信系统，$Q_S$通常大于1，由串联电路分压定律知，

$$ V_{L_S} =V_{C_S} =\frac{X_LE}{Z_T} = \frac{X_LE}{R} = Q_SE \tag{6} $$

　　电感或者电容上的电压比输入电压大很多，因此串联谐振电路中常常说电抗元件上电压升高Q倍。
　　对于串联RLC电路，在任意频率下的总阻抗为:

$$ Z_T= R+j(X_L-X_C) \tag{7} $$

4 $Z_T$随频率的变化

　　$|Z_T|$随时间频率变化的曲线如下图5所示：

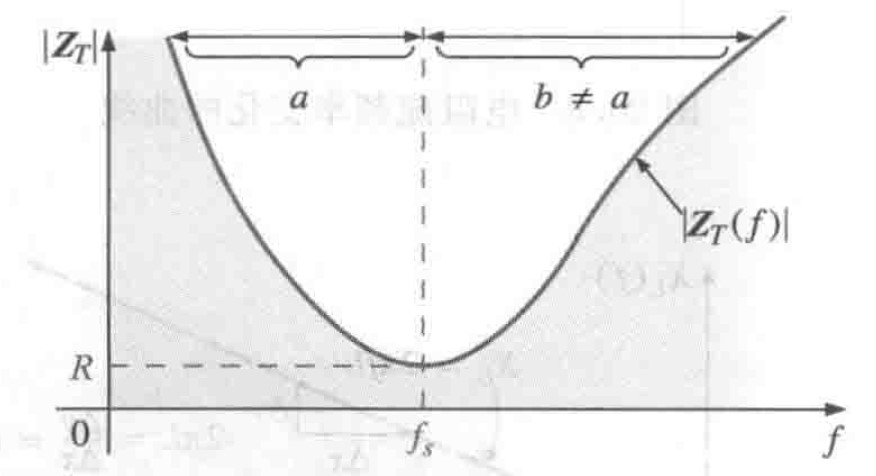图5 串联谐振电路的总阻抗模随频率变化的曲线

　　如图5所示，当$f< f_s$,电路为容性，电路为容性，电流超前于电压，当$f=f_s$，电路为纯电阻，电流与电压同相；当$f>f_s$，电路为感性，电流滞后于电压。

5 选择性

　　在电压E一定时，电流I随频率变化的曲线如下图所示：

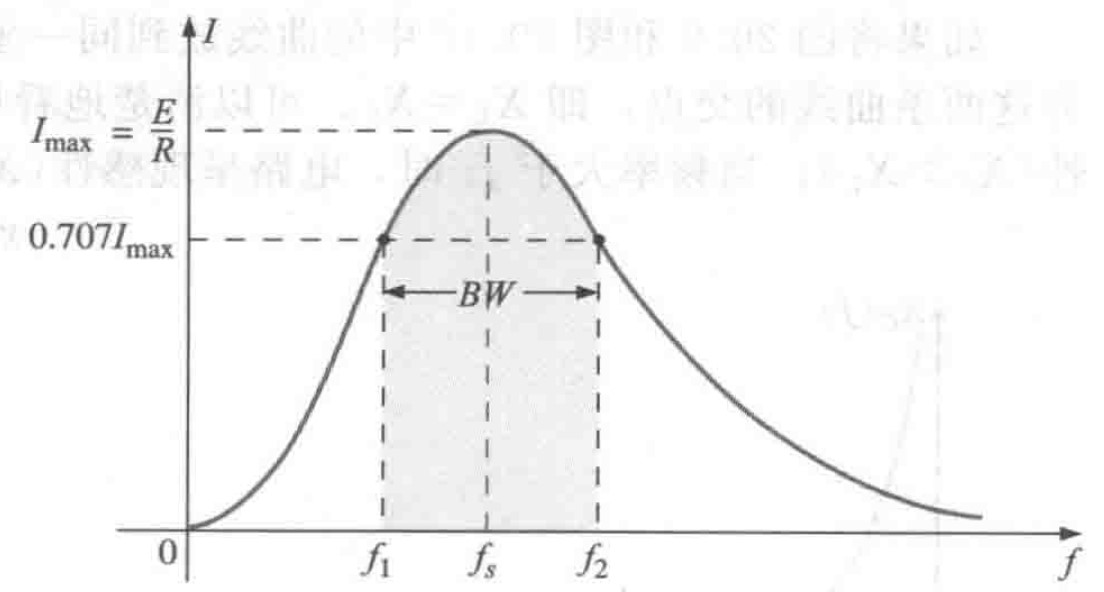图6 串联谐振电路电流I随频率变化的曲线

　　图6中给出了电流接近最大值而阻抗接近最小值的频率范围，对应于电流最大值的0.707倍的频率称为截止频率、半功率频率或转折频率（半功率频率是指传递的功率为谐振点功率（最大功率）一半时的频率）。在图中用$f_1$、$f_2$表示，这两个频率之间的范围称为谐振电路的带宽（缩写为BW）。
　　当$Z_T=\sqrt 2 R$时，可求出$f_1$、$f_2$，进一步得出

$$ BW = f_2-f_1= \frac{R}{2\pi L} = \left( \frac{1}{2\pi} \right)\left( \frac{R}{L} \right) = \left(\frac{f_s}{\omega _s} \right)\left( \frac{\omega _s}{Q_s} \right) = \frac{f_s}{Q_s} \tag{8} $$

　　公式(8)相当实用，因为他将电路的带宽与Q_s联系了起来，品质因数越大，带宽越窄。
　　因为谐振电路通过调谐来选择感兴趣的频带，所以图6中的曲线称为选择性曲线，当选择某一频率时，要确保该频率处于带宽之中，带宽越窄，选择性就越好。
　　而对于$Q_S$，$Q_S$越小，带宽越宽，选择性越差，$Q_S$越大，情况则相反。当$Q_S>=10$时，一般认为谐振频率处于带宽的中央，同时谐振曲线对称于谐振频率。

6 电压与频率的关系

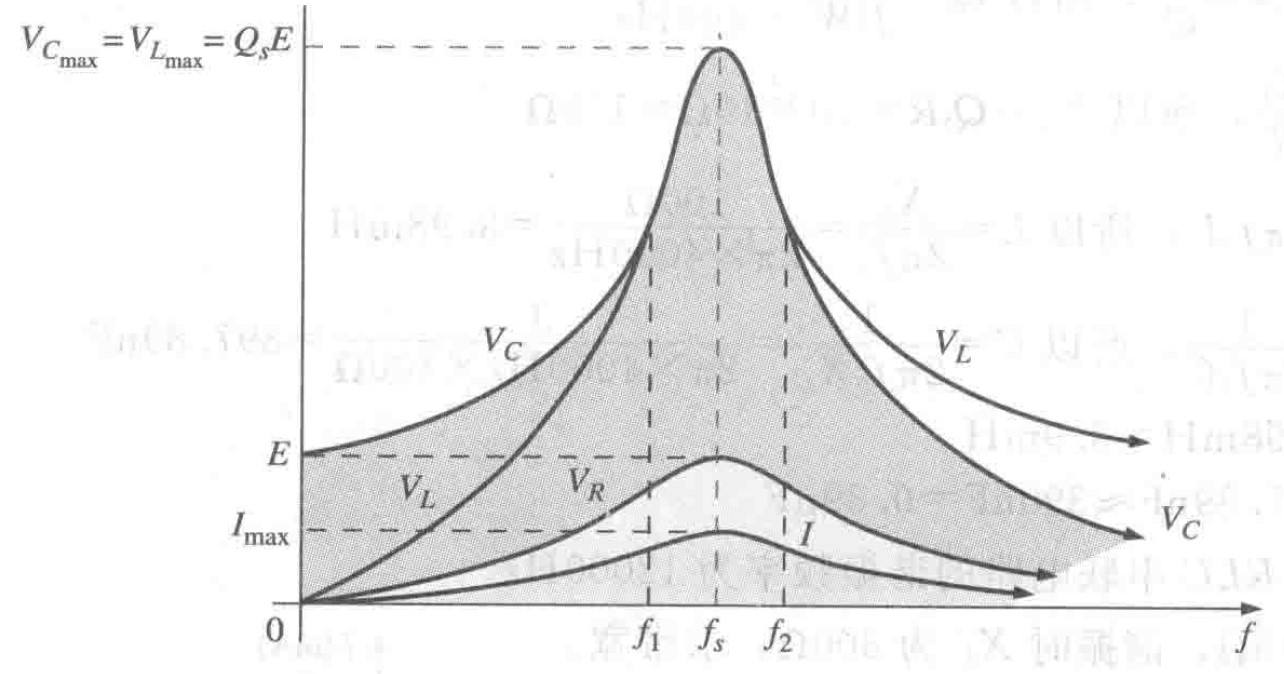图7 品质因素大于10时串联谐振电路中电压电流随频率变化的曲线
  1. $V_C$和$V_L$的最大值位于或接近谐振频率处（这取决于$Q_s$）
  2. 在频率很低时，$V_C$接近电源电压而$V_L$接近零，在频率很高时，$V_L$接近电源电压而$V_C$接近零.
  3. $V_R$和I均在谐振频率处取得峰值而两者的曲线形状相似。

7 并联谐振电路

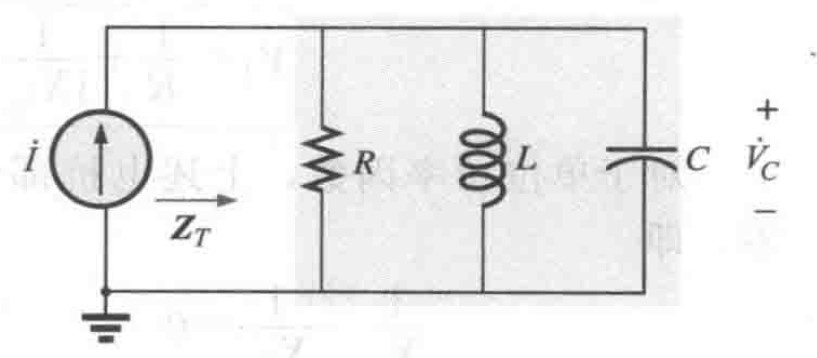图8 理想的并联谐振电路

　　对于如上图所示的理想并联谐振电路，当$X_C==X_L$时发生谐振，且谐振频率计算式与串联谐振时相同。
　　但是实际的电感是有电阻的，我们可以把RL串联组合等效为并联等效电路，如下：

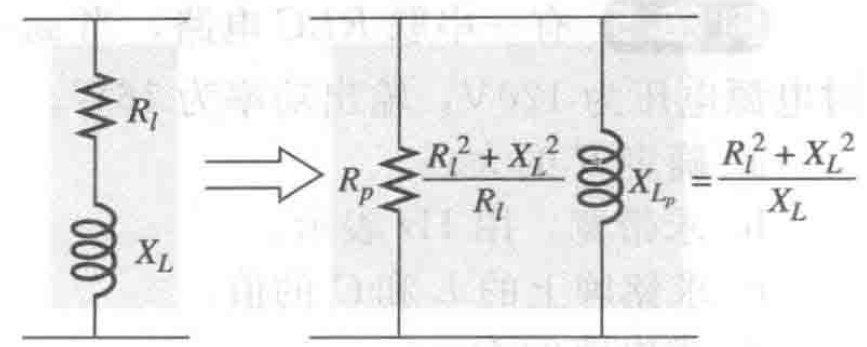图9 RL串联组合的并联等效电路
$$ R_P= \frac{R_L^2 + X_L^2 }{R_L} \tag{9} $$
$$ R_{L_P}= \frac{R_L^2 +X_L^2 }{X_L} \tag{10} $$

　　求出电感的等效电阻$R_p$，等效电感$X_{L_p}$，如下图所示：

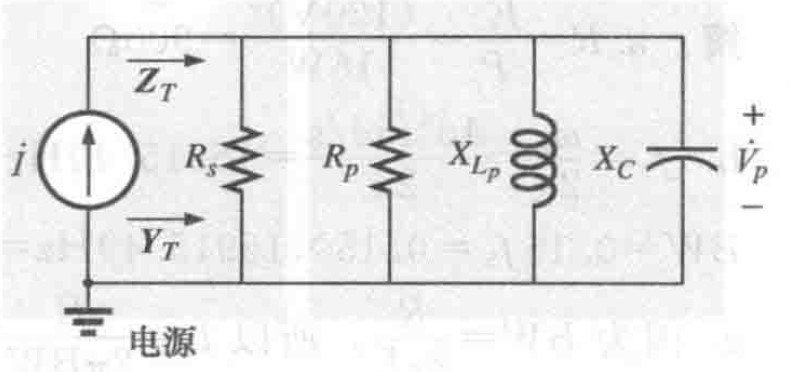图10 将串联RL电路等效成并联电路

　　最后，将电感的等效电阻$R_p$并上电流源内阻$R_s$，得到R，总的等效电路被转换为如图所示的理想并联情况：

图11 将图10中电阻用R替换之后的电路

　　在串联谐振电路中，阻抗为最小值时的频率为谐振频率，此时电流最大，输入阻抗为纯电阻，整个电路的功率因数为1。而对于并联电路，在等效模型中，电阻$R_p$是频率的函数，所以$V_C$达到最大值的频率和功率因数为1的频率是不同的，尽管两种情况都用来定义谐振的状态，但不同情况下的频率会有不同的下标表示。

8 单位功率因数的谐振频率

　　对于图11，当$X_{L_P}=X_C$时电路谐振，解得并联谐振电路在单位功率因数条件下的谐振频率

$$ f_p= f_s \sqrt{1 - \frac{R_L^2 C}{L}} \tag{11} $$

　　当$f=f_p$时，并联谐振电路的输入阻抗将接近但不等于最大值，因为$R_p$是频率的函数，在阻抗最大时，我们将频率定义为$f_m$

$$ f_m= f_s \sqrt{1 - \frac{R_L^2 C}{L}} \tag{12} $$
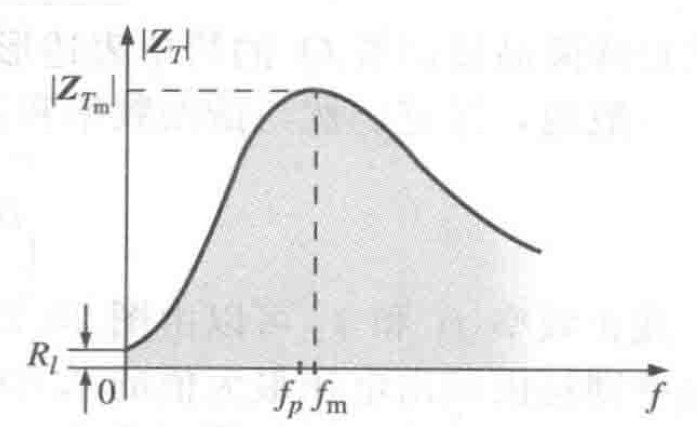图12 并联谐振电路中阻抗模随频率变化的关系

　　一般地：

$$ f_s > f_m > f_p \tag{13} $$

9 并联谐振电路的选择性

　　并联谐振电路中，当谐振时（频率为$f_m$）阻抗为最大，而不是像串联电路那样，谐振时阻抗为最小。

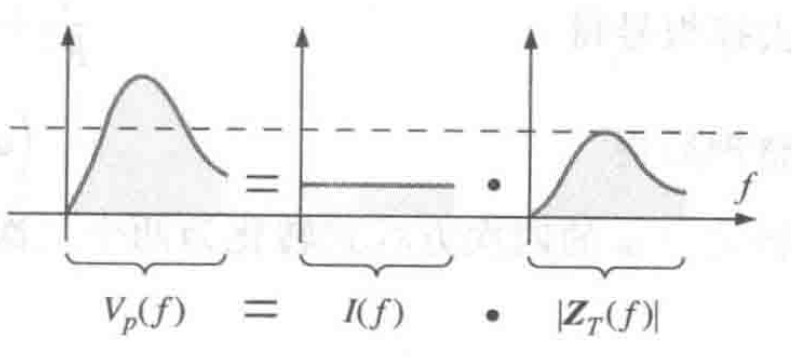图12 并联电压曲线的形状与阻抗模相似

　　并联谐振电路的品质因数的大小依然取决于无功功率和有功功率的比值，即

$$ Q_p=\frac{X_L}{R_L} \tag{14} $$

　　一般地，带宽仍然与谐振频率和品质因数有关，即

$$ BW=f_2-f_1=\frac{f_r}{Q_p} \tag{15} $$

　　截止频率$f_1$和$f_2$由半功率频率求出，解出得：

$$ f_1=\frac{1}{4\pi C}[-\frac{1}{R}+\sqrt{\frac{1}{R^2}+\frac{4C}{L}}] \tag{16} $$
$$ f_2=\frac{1}{4\pi C}[\frac{1}{R}+\sqrt{\frac{1}{R^2}+\frac{4C}{L}}] \tag{17} $$

　　在频率很低时，容抗很大，感抗很小，由于元件相互并联，因此总阻抗在低频时呈感性。在频率很高时，情况则相反，整个电路呈容性，按照单位功率因数条件谐振时，整个电路得输入阻抗为纯电阻，下图描述了阻抗角与频率得变化规律。

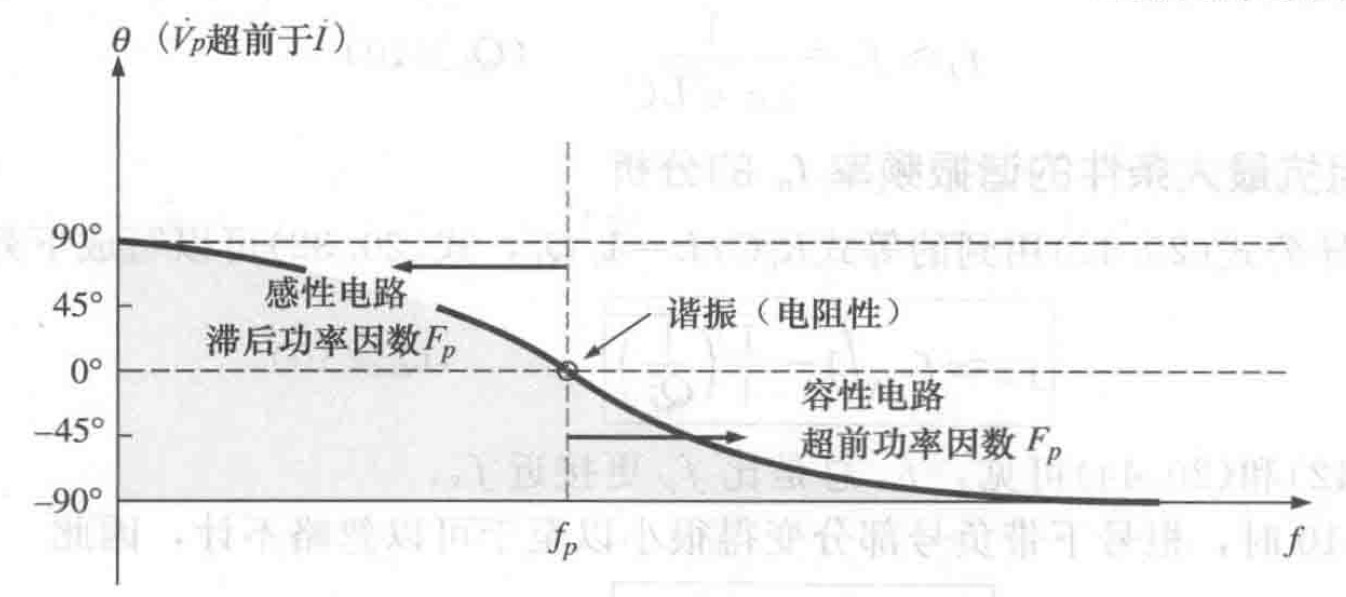图12 并联谐振电路电压和电流的相角差与频率的关系

10 高品质因数对谐振的影响

　　从前一节可以看出并联谐振电路比串联谐振电路复杂很多，但是只要品质因数$Q_L$足够大（例如大于等于10），就可以用许多近似方法来简化分析。
　　当$Q_L>=10$,不考虑电感的复杂性了。

$$ X_{L_p}\approx X_L=X_C \tag{18} $$
$$ f_m=f_s=f_p \tag{19} $$

　　品质因数越高，他们三个就越接近。

二 分贝、滤波器和伯德图

1 分贝

　　功率增益中，分贝的定义为:

$$ dB=10lg\frac{P_2}{P_1} \tag{20} $$

　　可以看出，分贝其实是两个功率的比值，在通信中，一般定义$P_{ref}=1mW$(输送给600欧的负载)，那么此时

$$ dB_m=10lg\frac{P}{1mW}|_{600\Omega}\tag{21} $$

　　下标m表示以1mW为参考值的分贝数。
　　电压增益中，分贝定义为：

$$ dB_v=20lg\frac{V_2}{V_1} \tag{22} $$

　　上式中下标v用来表示电压的分贝数。

2 RC低通滤波器

　　RC低通滤波器如图，如果将电容电压作为输出，那么他就是低通滤波器，如果将电阻电压作为输出，那么他就是高通滤波器

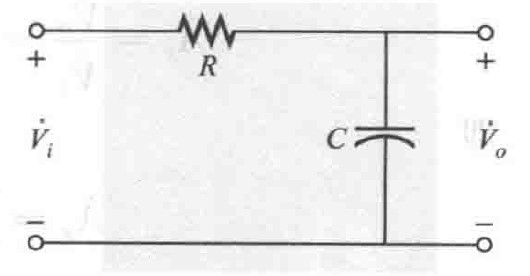图13 RC低通滤波器

　　归一化是指一些参量如电压、电流或阻抗，除以和他们具有相同单位的某个量，从而得到大小在特定范围的无量纲的量。

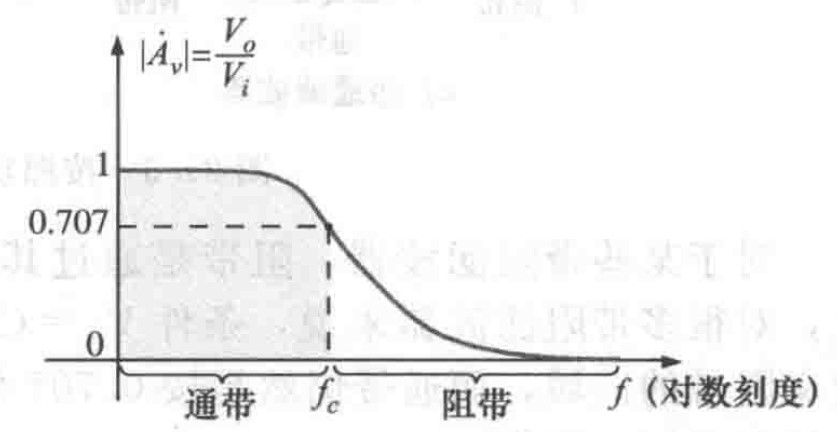图14 幅频曲线归一化之后图像

　　计算得到截止频率:

$$ f_c=\frac{1}{2\pi RC} \tag{23} $$

　　对于任何低通滤波器，任何频率低于$f_c$的输入电压，产生的输出电压$V_o$都将大于最大值的70.7%；而任何频率高于$f_c$的输入电压$V_o$都将小于最大值的70.7%。
　　电容输出的电压$V_o$一直滞后于$V_i$，滞后角度如图所示：

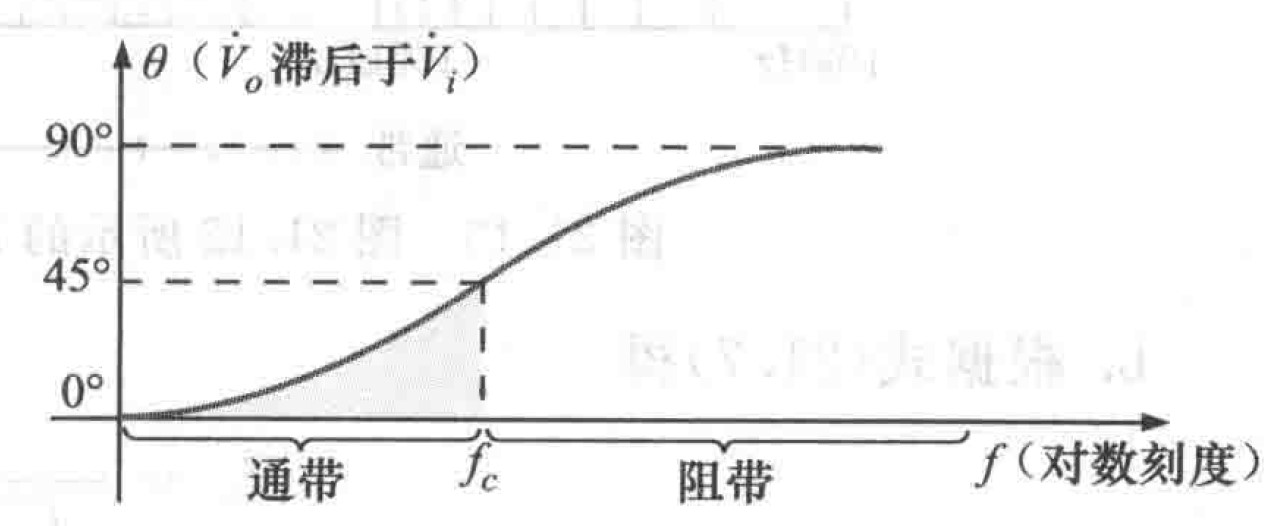图15 输出电压滞后于输入电压的相角

3 RC高通滤波器

　　交换RC低通滤波器中电阻和电容的位置，即可构成RC高通滤波器。输出电压的模值和相位推理方法同上节RC低通滤波器，应用串联电路分压定律即可得到，总之，对于RC高通滤波器，有

$$ f_c=\frac{1}{2\pi RC} \tag{24} $$

　　当$f< f_c$时，$V_o< 0.707V_i$; 当$f>f_c$时，$V_o>0.707V_i$;当$f=f_c$时，$V_o$超前于$V_i$ 45°;

4 带通滤波器

　　一种最直接得到带通滤波器的方法就是利用串联或比关联谐振电路的选频特性，在通带内总有$V_o>=0.707V_{max}$。实际应用中，可假设谐振频率平分带宽，这种近似通常是可以接受的。
　　另一种得到带通滤波器的方法就是将一个高通滤波器与一个低通滤波器级联起来，如下如图：

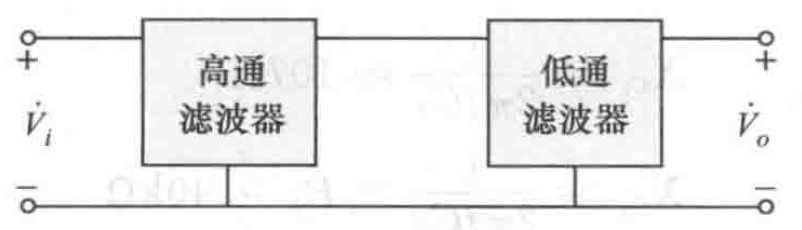图16 级联式带通滤波器

5 带阻滤波器

　　带阻滤波器的特性与带通滤波器的特性正好相反，因此从串联谐振电路的的电阻上取输出，或从并联谐振电路的串联电阻上取输出，就可以得到带阻滤波器。

6 伯德图

　　通过直线段来高效来且相当准确地表示系统的频率响应，这样的一种幅度和相位随频率变化的曲线叫做伯德图。对于伯德图的更多研究，此处不再赘述，需要应用时再去深入研究。

7 交叉式分频网络

　　为了滤波器性能更好又不适用高复杂性的设计，常常使用分频网络，分频网络常被应用于音频系统，以此确保合适频率的信号传输到恰当的扬声器，使得低音、中音、高音响应更好。