一 信号

1 引言

　　本系列的主题是现代电子学，他被认为是微电子学的领域。微电子学指的是集成电路技术，现在的集成电路技术能在$100{mm}^2$量级的一小片硅上生产含有数百万个元件的电路。例如，这样的一个微电子电路就是一个完整的数字计算机，也被称为一个微型计算机，或者更通常地说是一个微处理器。
　　在我开辟这个模拟微电子系列，我将介绍电子器件，这些器件既能够单独使用（在分立元件电路的设计中），也可以作为集成电路芯片的元件使用，还将讲解如何设计和分析器件之间的互连，这些器件组成的分立元件和集成电路可具有不同复杂度和不同功能。此外，还将介绍已有的集成电路芯片及其在电子系统设计中的应用。
　　作为本系列的第一篇博客，主要介绍一些基本的概念和术语，特别是讲解信号及其利用电子电路实现的最重要的信号处理功能之一——信号放大，然后介绍线性放大器的模型，在后续几章中将采用这些模型。

2 信号

　　自然界的信号都是模拟信号，首先需要换能器将这些自然界的物理量转换成电信号，然后再由电子系统来对信号进行处理，其中放大器是模拟电路的基本元素，逻辑反相器是数字电路的基本元素。信号（y轴）——时间（x轴）这样一个函数可以转换到频域去分析。傅里叶级数可以将周期信号表示成无数个正弦波的叠加，反映在频谱上就是一个一个离散的冲激响应。
　　傅里叶级数的公式、概述在电路分析复习笔记(4)已经列出，这里就不重复，傅里叶变换具有更好的通用性，它可以将任意时间函数转换到频域，反映到频谱上就是一个连续函数（实际信号重要的只是频率轴上较短的一段）。关于傅里叶级数和傅里叶公式的系数的含义，以及他们的物理含义特别重要，这些内容我将放在信号与系统中深入讲解。

二 放大器

1 基本概念

　　电压放大器：只放大电压。用分贝表示的电压或电流增益如下式

$$ A_v=20lg\frac{V_o}{V_i} \tag{1} $$

　　功率放大器：不放大电压，只放大电流。用分贝表示的功率增益如下式：

$$ A_p=10lg\frac{p_o}{p_i} \tag{2} $$

　　对电压增益和电流增益取绝对值是因为在某些情况下电压(电流)输出与输入的比值可能是负值，一个负值只表明输入和输出有180°的相位差，并不是指放大器会减弱信号，但是若最后按照上式求出的总增益为负数，则表明放大器会对输入信号进行衰减。
　　放大器对信号放大，能量来自于直流供电的电源，对于一个放大器，输入的能量有从信号源得到的功率$P_I$,从直流电源得到的功率$P_{dc}$，输出的能量有传输给负载的功率$P_L$，放大器损耗的功率$P_{dissipated}$，

$$ P_{dc}+P_I=P_L+P_{dissipated} \tag{3} $$

　　其中放大器从信号源那里得到的功率一般很小很小，可以忽略不计，因此放大器的效率定义为：

$$ \eta=\frac{P_L}{p_{dc}}\tag{4} $$

　　放大器饱和：放大器的输出电压有一个正极限和一个负极限，称为正负饱和电平，即使在饱和电平内，放大电压也不一定是线性的，只有在输入幅度足够小且偏置正确的情况下，放大才是线性的，此时的斜率就是放大倍数。

2 符号含义：

  • 总的瞬时量用小写字母和大写下标表示；
  • 直流量用大写字母和大写上标表示；
  • 增量信号用小写字母和小写下标表示；
  • 正弦信号用大写字母和小写下标表示；
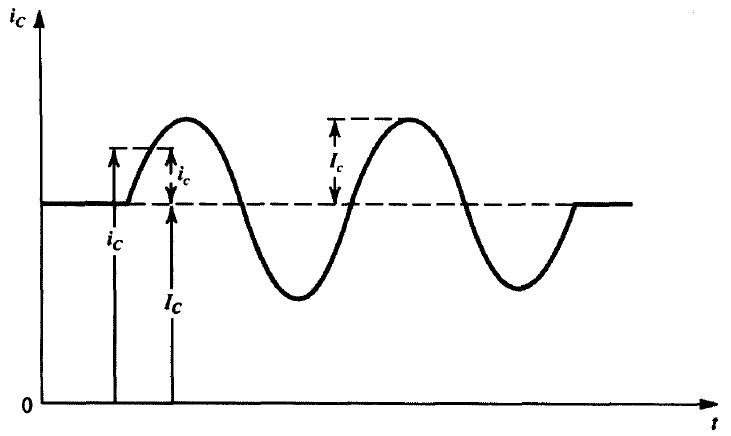图1 符号示例

三 放大器电路模型

1 电压放大器

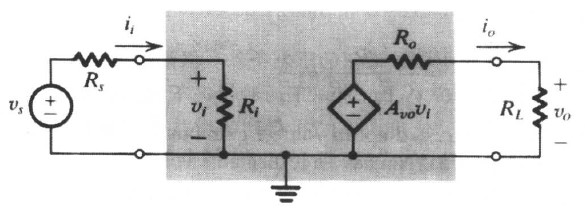图2 电压放大器模型

　　在设计放大器时，为了不丢失输入信号，使负载得到的电压尽可能大，放大器的输入电阻$R_i$必须尽可能大，输出电阻$R_o$必须尽可能小，远小于负载电阻，如果负载电阻未被指定，那么通常假设给出的电压增益是开路增益$A_{v_o}$。

2 级联放大器

　　放大器经常设计成多级，每一级功能都不相同，第一级要有较大的输入电阻，第二级有较高的增益，最后一级有较低的输入电阻。

3 四种类型放大器

图3 四种放大器类型

　　以上四种类型放大器，可以相互转化。

四 放大器频率响应

　　放大器的传输函数包括幅频曲线和相频曲线。

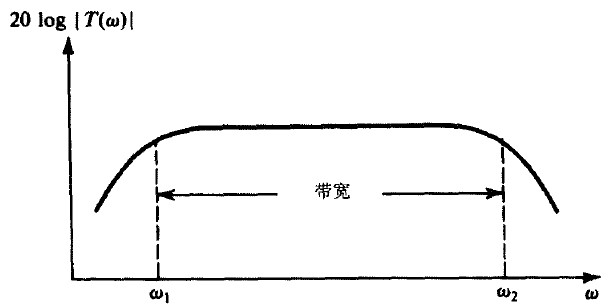图4 一个典型的放大器频幅响应

　　在一定范围内，即$\omega_1$到$\omega_2$，放大器的增益几乎不变，或者有一定程度的降低（通常是3dB）,这一段范围称为放大器的带宽，我们放大器的带宽与所要放大信号的频谱相重合。

五 数字逻辑反相器

　　逻辑反相器是数字电路设计中最基本的元素，就像模拟电路中的运算放大器一样。
　　反相器的电压传输特性曲线如下：

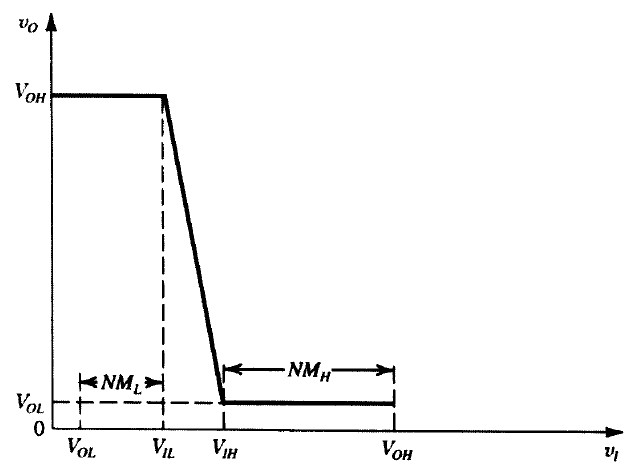图5 反相器的电压传输特性曲线
  • $V_{OL}$:输出低电平；
  • $V_{OH}$:输出高电平；
  • $V_{IL}$:被反相器认为是逻辑0的最大输入电压值；
  • $V_{IH}$:被反相器认为是逻辑1的最小输入电压值；
  • $NM_L$:输入低电平噪声容限；
  • $NM_H$:输入高电平噪声容限